Navigation:  Prospect/Field evaluation > Entering probability distributions > Input Variables > Shape Factor

See also 'Entering Probability Distributions'.

 

The Shape Factor term in the Area-Thickness-Shape factor model for gross rock volume is there to account for geometrical and edge effects.

 

Suppose you have a perfectly hemispherical reservoir of radius r. The area on the map (looking down from above) is pi.r.r. If you multiply by a thickness h you get the volume of a cylinder pi.r.r.h. Since we assume it is a hemisphere, then h=r and the volume is pi.r.r.r.

 

But we know that the reservoir volume is actually that in the hemisphere, which is 2/3.pi.r.r.r. So in this case the shape factor is 2/3, or 0.67. In the case of a pyramid, the shape factor is 1/3, or 0.33.

 

In both of these cases, it is assumed that the reservoir thickness is at least as big as the closure (the closure being defined as the depth from the highest point in the reservoir to the water contact).

 

If the reservoir is less than the closure, the shape factor is higher. When the reservoir is very thin compared to closure the shape factor is almost 1.0

 

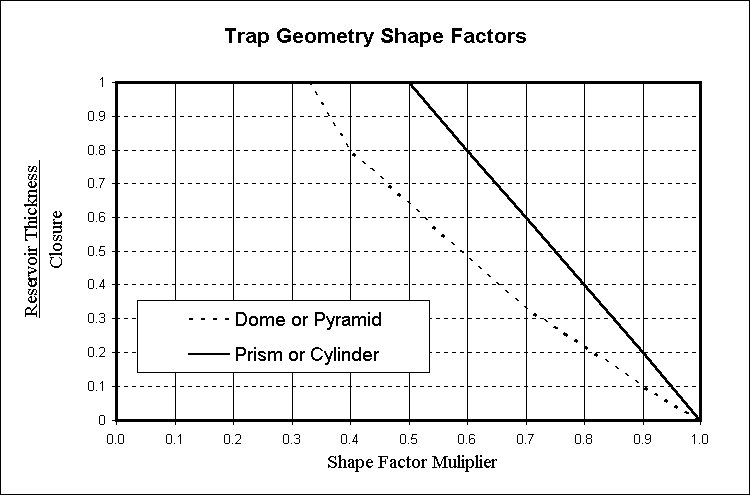
The figure below can be used to estimate the shape factor. Work out the ratio of reservoir thickness to closure, look that up on the y-axis, go across to the shape you have, and read the shape factor on the x-axis. The problem is: what is the shape? With the hemispherical reservoir above, you would probably say: my reservoir is like a dome, so I'll use the dome shape. And the figure says that for a reservoir thickness/closure of 1.0, the shape factor is 0.33. But we just worked it out to be 0.67. So using the figure you are wrong by a factor of 2.

 

The moral of this is: only use area/thickness/shape factor for GRV when the reservoir is thin compared to closure (i.e. shape factor is nearly 1.0); or you have so little data you have no choice. If you do have data, use the area/depth model and get it right!