Navigation:  Consolidations > Input parameters > Common chance

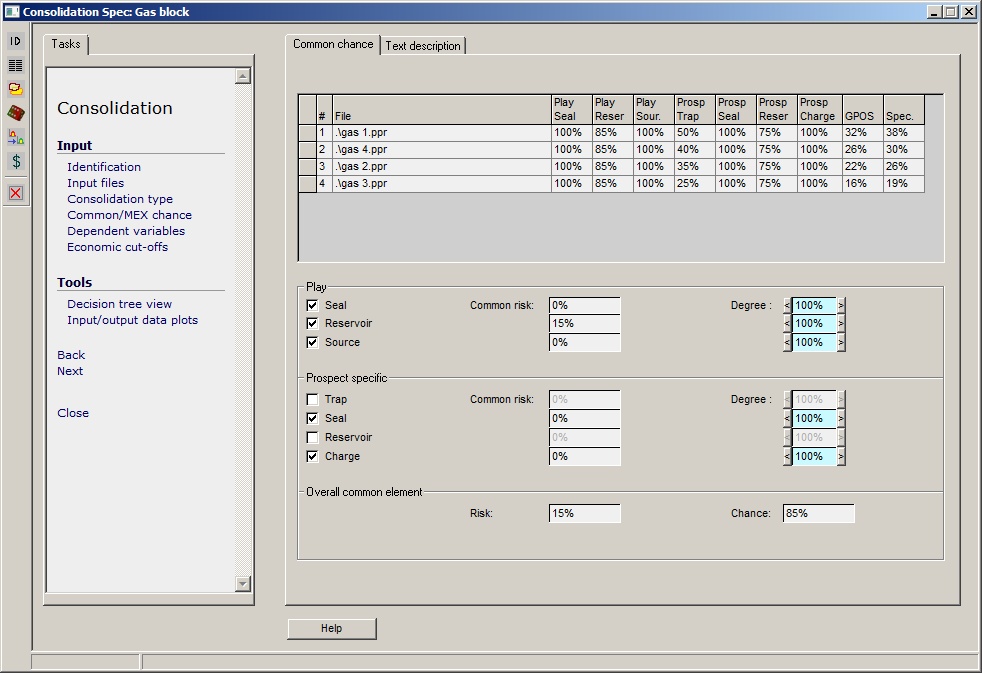
If you are consolidating with common chance (also referred to as common risk) you must enter those elements of input prospect chance (if any) are common to all the prospects. This is done on the Common Chance dialog, shown below,  in the "Common/MEX chance" page of the consolidation input.

The actual dialog you see will depend on the risking scheme you are using. The one below is for scheme 9. Not all schemes allow you to specify partial dependencies, so the main difference between dialogs (apart from the risk names) is whether you see the slider bars on the right.

For each entry in the consolidation the elements of overall prospect chance are specified. (Remember that the input may also be the result of a consolidation.)

Below the table of inputs, check those elements that are common. The common risk for each risk element is the amount of risk which is common. The most than can be shared for any element is minimum risk of all the input elements in that category.

In the example below, and remembering that Risk = 1  - Chance:

·You cannot share any regional (play) seal risk because there isn't any - the chance for both inputs is 100%. Ditto regional reservoir and source.

·For the prospect specific reservoir risk, you can share 25% of risk - both input chances are 75%

·For the prospect specific trap risk "gas 1" has a risk of 50% and "gas 4" a risk of 60%. The most you can share is 50%.

You can specify how much of the potential shared risk you actually share (this is not available for all risking schemes). Sharing is in steps of 25%.

The program updates the Overall common elements (Risk and Chance) entry automatically. It will also update the Specific column (which is the specific chance for the input - i.e. the chance with the common elements removed).

[Note: For consolidations of prospect segments, the play chance is defined to be common to all inputs. Therefore the select element entries for reservoir, source and seal play chances are set to 'yes' and cannot be altered.]

 

 

There is a tab to enter comments. It is strongly recommended that you explain you choices of common risk.

If the risking scheme you are using has an amplitude modifier, the combination of entered common chances may be invalid. If so, the common chance is shown in red. Were you to try a calculation it would not complete. See Common chance with an amplitude modifier below.

Consolidation Calculations

The results of consolidation calculations are more sensitive than prospect calculations to the number of iterations used. This is especially so when some or all of the inputs are high risk.

The number of iterations to be used is specified in the set-up and defaults. If the program thinks that the number chosen will give insufficient resolution then it will increase it.

The differences between the various forms of consolidation and the principle of common chance which underlies them is probably the most difficult concept in the program.

Common chance is present if the outcome of one prospect (hydrocarbon discovery or not) affects the chance of success of one or more other prospects.

If this is not the case then use the simplest form of consolidation, a General consolidation, to add the prospects. With this method, input distributions are simply summed up after adjustment for the overall chance of each input. Under certain circumstances this can give very misleading results.

Consider the example of identical prospects in a play, each with a play chance of 60% and a prospect specific chance of 20% - giving an overall chance for each prospect of 12%.

If three of these prospects are consolidated using a general consolidation, the chance of finding at least some hydrocarbon (i.e. the chance of success) is:

1 - { (1-0.12) x (1-0.12) x (1-0.12) } = 32%

If two more identical prospects are added to the play the chance of success goes up to 47%. If there are ten prospects it goes up to 72%. With a hundred there is a near certainty of discovering oil.

The trouble is, we assumed that the prospects were all in the same play, and that the play chance was 60%, which means there is a 40% chance that the play doesn't work at all. And if it doesn't then all the prospects fail - regardless of how many there are. So the greatest the chance of success can ever be is the play chance.

The figures given for the general consolidation case above are correct only if all the prospects are in different plays; in other words, if they are completely independent. And we can define independence:

Prospect B is independent of prospect A if the outcome of drilling A (success or failure) does not influence in any degree the probability of success or the predicted reserves distribution in B.

In the example above, the prospects are dependent because they are all in the same play. If the first one is drilled and is a failure, it may or may not change the play and prospect chances of the others (depending on why it was a dry hole). But if it is a success it definitely will, because the play becomes proven, and the play chance in all the other prospects becomes 100%.

To get the correct answer when consolidating our prospects in the unproven play we first remove the common chance from each prospect's overall chance. The common chance being the play chance, we are left with just the prospect specific chance. The prospects are now "independent" and we can consolidate them. Then at the end we factor back in the common chance.

In our three prospect example:

1.Remove the play chance: each prospect has a specific chance of 20%.

2.Calculate the chance of success of the "independent" prospects: ICOS = 1 - { (1-0.2) x (1-0.2) x (1-0.2) } = 49%.

3.Factor back in the 60% play chance: COS = ICOS x 0.6 = 29%.

With 5 prospects the chance of success is 40%, and with 10, 54%.

This is the method that REP uses when consolidating prospects in a play.

More subtlety is available because both play chance and prospect specific risk are themselves composites. Play chance is divided into reservoir, seal and source chances; prospect specific chance into trap, reservoir, seal and charge chances. Depending on the circumstances, some or all of these chances can be defined as common between inputs to a consolidation.

 

 

Consolidation Forms

The circumstances that are recognized by REP are:

1. Segments in a Prospect

Prospect segments are areas of a prospect which have different (or - more properly - not necessarily identical) prospect specific risks.

For example, you may have a prospect with a fault up the middle. Drilling one side of the fault may not (and most probably does not) prove the existence of hydrocarbon on the other. Before any drilling, the prospect specific risk of each segment may or may not be the same. If you drill a successful well in one segment, the prospect specific risk of that segment becomes 100% (proven). The chance of hydrocarbon in the other segment most probably increases, but not to 100%. In other words, by hitting good in segment A you remove some of the risk from segment B, but not all of it. In terms of individual chances before and after drilling A you might have something like:

 

Examination of this table shows the following:

Before drilling, the trap chance in B is lower (riskier) than in A. After drilling A, B's trap chance increases, implying that some elements of the trap risk are common to both A and B.

After drilling A, the reservoir chance in B goes to 100. This means that the reservoir chance elements in A are the same as B and proving A's reservoir also proves B's. The reservoir chance is therefore common. The same is true of the migration chance.

Proving A's seal does not alter the chance of a seal in B. Therefore the seal chances are independent (not common).

Note: Risks are either common or not, there is no allowance for degree. You cannot say that 50% of the trap chance in A is shared with B; it is all or nothing. The segment with the highest chance determines the common chance.

Also, if you specify a chance to be common, it is common to all the prospects being consolidated. Separate consolidations must be made, and the consolidations consolidated, if this is not the case.

By definition, segments of a prospect must be in the same play; therefore, the play chance elements for each segment must be common.

2. Prospects in a Play

In this consolidation, all of the play chances are common, but none of the prospect specific chances are. You cannot link (or unlink) individual risk elements.

3. Stacked Plays

This form of consolidation envisages plays stacked in a vertical sense, perhaps being tested by a single well - though of course this need not be the case. The prospects to be consolidated are in different plays, and their prospect specific chances are not common. However, some or all elements of the play chance (reservoir, seal and source) may be made common to all the prospects.

4. General

In general consolidations there is no common chance.

5. Stacked Prospects

This is the most flexible form of consolidation, in the sense that any or all of the individual chance elements may be made common. The geological realisation of the circumstances in which combinations of play and prospect risks may be made common or not is left to the user.

Another Example

There are three prospects being consolidated, P1, P2 and P3, with chances as shown in the table. The common chance row is in red and shows the common chance for each category, should that category be defined as common. Note that where any of the individual prospect chance in any category is 100%, there can be no common chance (no common chance is equivalent to a common chance of 100%: if this seems odd, think of it in terms of risk. If there is no risk (chance=100%) there is no risk to share).

Now look at the consolidation cases:

1. A General consolidation: by definition there is no common chance.

2. A consolidation of Prospects in a Play: only play chances are common (and in this case, only the reservoir has any risk so making the seal and source chances common has no effect).

3. & 4. These are Stacked Prospect consolidations. In case 3 an arbitrary selection of chances are made common. In case 4, everything is common. But even in case 4 there is still some "residual" risk (for example, prospect P2 still has only a 50% chance of a successful charge even if the common element of the charge chance (80%) is proven). That is why the common chance is not the same as the GPOS.

 

Common chance with an amplitude modifier

The operation of common chance is more complicated if the risking scheme allows an amplitude modifier. This is because the modifier A is an addition (or subtraction) to the "standard" multiplicative geological chance G. (Note, if the thought of an equation make you feel weak at the knees, skip to the last two paragraphs of this section.)

 GPOS        =  G + A

         =  Gtrap x Greservoir x Gsource ....etc.   + A

For consolidation the GPOS for each prospect is divided into a common element Cm and a specific element Sp:

 GPOS        =  Cm x Sp

 

As described above in the section on consolidation calculations, the common chance is "taken out" of the GPOS for each prospect, the prospects consolidated using the specific chance, and the common chance reapplied at the end to the final result. For this to work with an amplitude modifier it must be converted to a multiplicative factor A':

 GPOS        =  G + A

         =  G x A'

 A'        =  1 + (A/G)

and the calculation can use A' as if was just another chance.

 

The problem is that sometimes it cannot work. Consider a prospect with G=48%, A=20% and so GPOS=68%

 A'        =  1 + (0.2/0.48)

         =  1.42

Now suppose you make G common and A not:

 GPOS        =  Cm x Sp

 0.68        =  0.48 x Sp

So the specific chance = 0.68 / 0.42 = 142% - which is not definitely not allowed!

 

You can think of the amplitude modifier as a quantitative way of modifying one or more of the underlying geological chances - it is not a risk itself. Therefore if you say: the underlying active geological chances are all common, it is necessarily the case that the amplitude modifier must also be common. Similarly, if you say that the amplitude modifier is common, then at least some of the geological risk must be common - enough, in fact, to ensure you don't get chances greater than 100%.

 

In the common chance entry dialogs, the common chance goes red if the combination of specified common chances is invalid.